Shear and Buoyancy
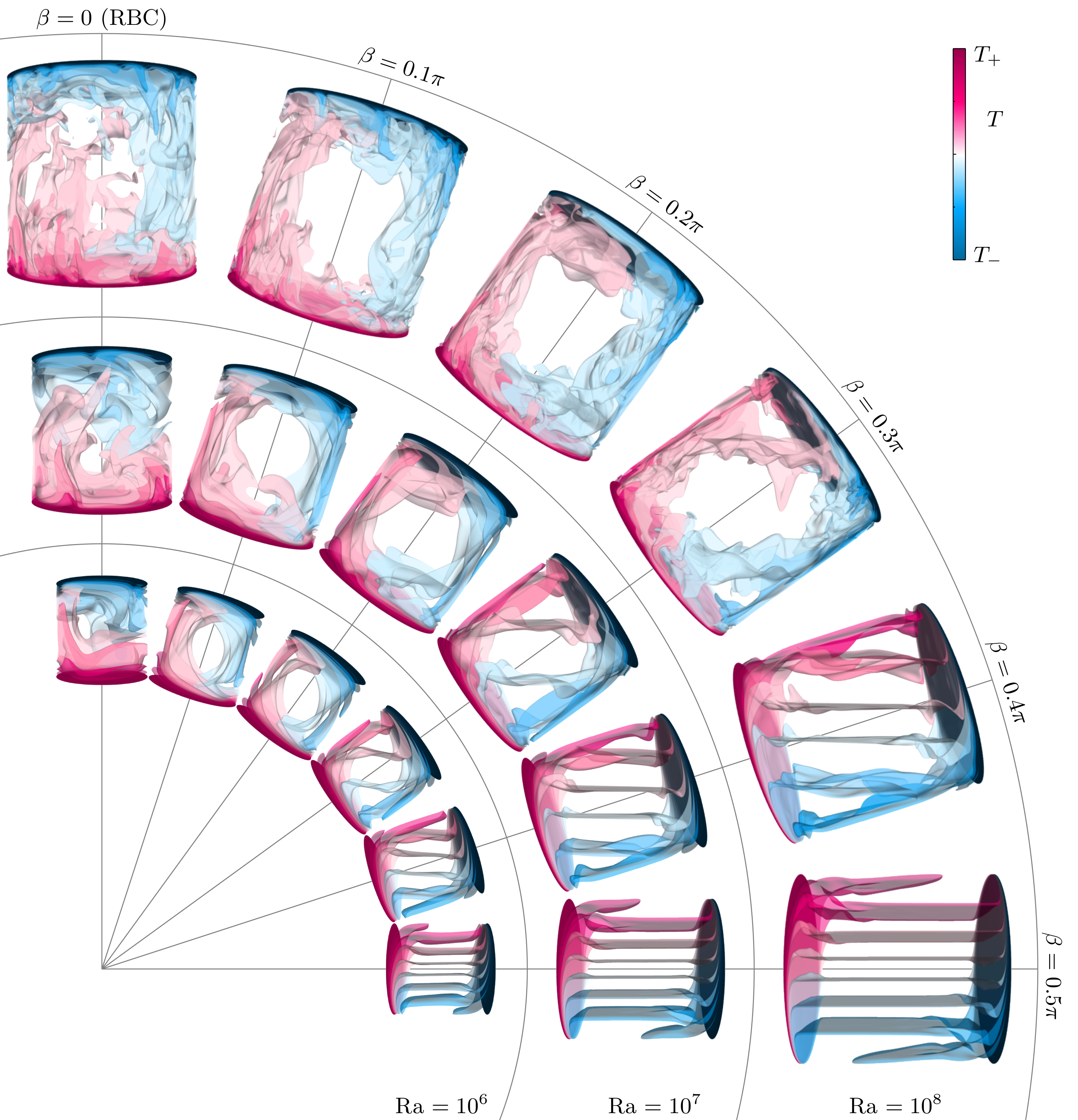
In inclined convection a fluid layer is tilted with respect to the gravity direction, and thus, not only buoyancy, but also shear drives the flow in this case. An inclination angle of β=0 corresponds to Rayleigh–Bénard convection, i.e. a fluid heated from below and cooled from above, and β=π/2 corresponds to vertical convection, where a fluid layer is confined between vertically aligned heating and cooling plates. The heat flux dependence on the inclination angle is not universal and is a also a complicated non-monotonic function of the Rayleigh and Prandtl number. Moreover, a slight cell tilt may not only stabilise a large scale circulation but can also enforce one for cases where the preferred Rayleigh–Bénard state is a more complicated multiple roll state.
In liquid metals a strong heat flux increase is observed in the case of inclined convection (see figure below). For liquid sodium the increase is almost 20-30% at the optimal inclination angle compared to RBC case and even for vertical convection (β=π/2) the heat flux is incresed by about 10%. This strong increase is only observed in low-Prandtl number fluids, like liquid sodium. The increase for the case of Pr=1, Ra = 109 is only approximately 6% at optimal inclination angle.
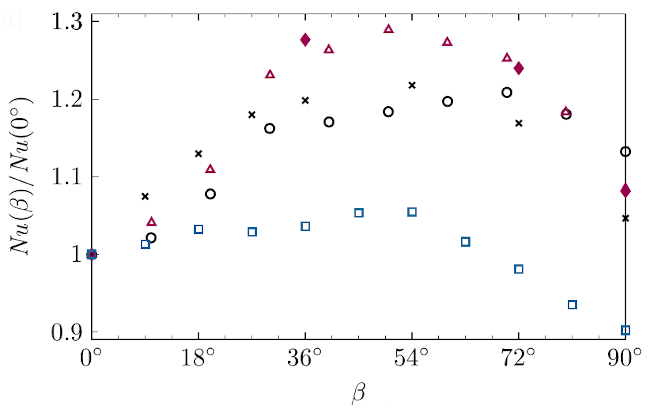
The reason for the strong increase in inclined liquid sodium convection is the suppression of the so-called twisting and sloshing modes (see the video below). In the case of RBC the phase of the large-scale circulation close to the heated plate shows a anti-correlation compared to the phase at the cooled plate. This comes along with a strongly varying instantaneous heat flux. However, inclination suppresses these modes, which leads to a less varying and more efficient heat flux.
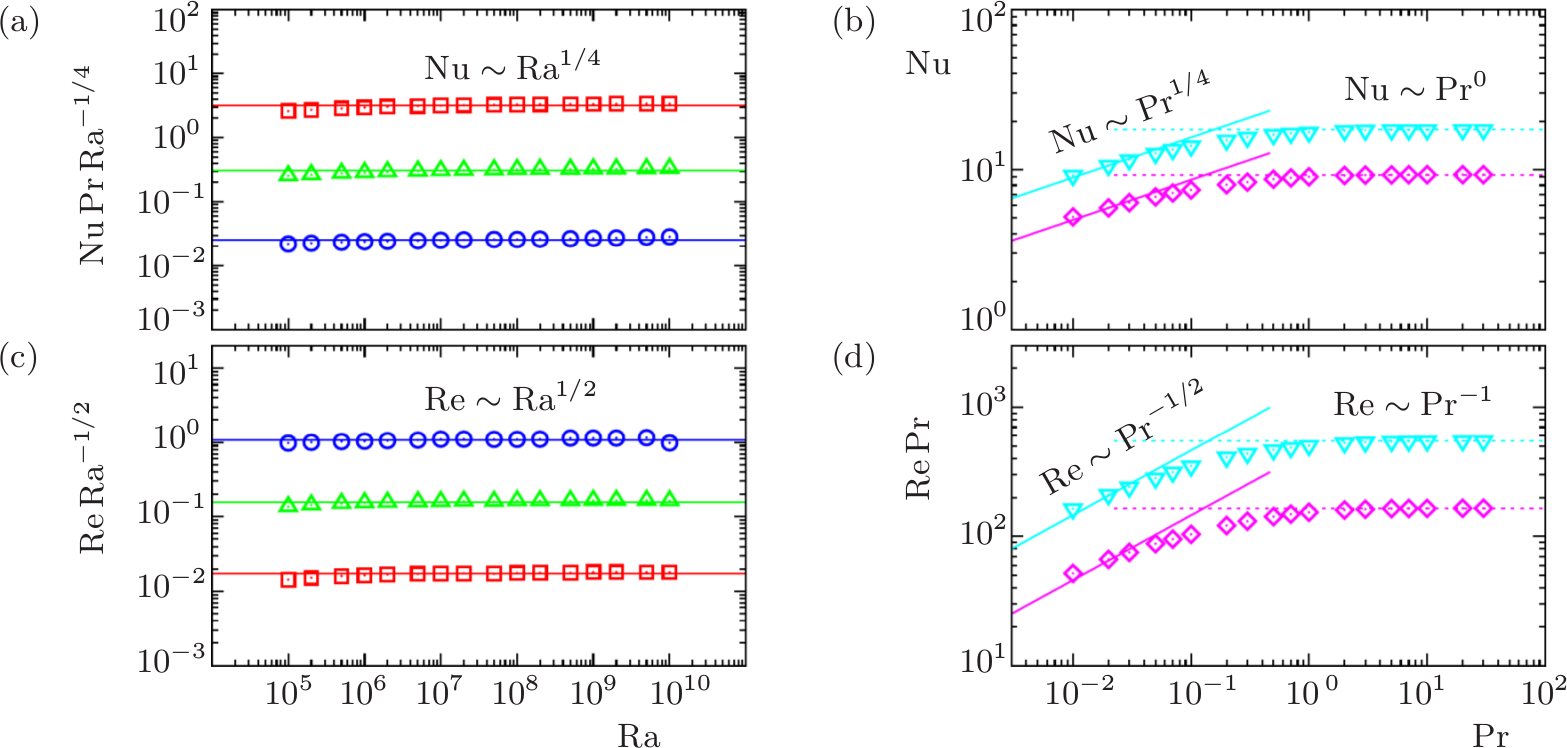
In the case of laminar vertical convection (β=π/2) it is possible to derive the dependence of the Reynolds number Re and the Nusselt number Nu on the Rayleigh number Ra and the Prandtl number Pr by advancing the Prandtl boundary layer theory,
see Shishkina, PRE 93 (2016).
This yields two limiting scaling regimes: Nu ~ Pr1/4 Ra1/4, Re ~ Pr –1/2 Ra1/2 for Pr≪1
and Nu ~ Pr 0 Ra1/4, Re ~ Pr –1 Ra1/2 for Pr≫1.
DNS show that the transition between the regimes takes place for Pr around
Further reading